Contents

• 1. Introduction and Purpose
• 2. Description
• 3. Control Form - Operation
• 3.1 Operation - Control Form # BH = 1
• 3.2 Operation - Control Form # BH = 2
• 3.3 Operation - Control Form # BH = 3
• 4. Display Form - Operation
• 5. Menu Form - Operation
• 6 Simulation of BH merger
• 7. VB2019 Simulation of Binary Black Hole system, circulated by a third star

Reflection

• Reflection 1 - Overall evaluation of this simulation
• Reflection 2 - Gravitational waves - three questions
• Reflection 3 - Does the concept: "Gravitational waves" makes sense ?

Visual Basic program "VB2010 BHmerger" & "VB2019 BHmerger"- Description and operation

1. Introduction and Purpose

The purpose of the Visual Basic program "BHmerger" is to demonstrate:

1. That it is possible that photons can circulate around a blackhole
2. What is involved if two Black Holes merge.
3. The influence of a third BH.

To download an executable select: VB2010 BHmerger.zip
This zip file contains 1 program:

• "VB2010 BHmerger.exe" written in Visual Basic 2010.

The same program is also available in Visual basic 5.0. To download an executable select: VB BHmerger.zip
This zip file contains 1 program:

• "VB BHmerger.exe" written in Visual Basic 5.0

For a description of that program select: Visual Basic program "VB BHmerger" - Description and operation

For more information goto: Implementation details

2. Description

The Visual basic program "VB2010 BHmerger" & "VB2019 BHmerger"consits of 2 Forms (or displays):

• Control Form. This form is used to Start the program and to modify the parameters.
• Display Form. This form shows the results of the simulation in a graphical form.

3 Operation - Control Form

Operation of the program is done from the Control Form.
The Controm Form uses 5 Commands: Start, Cont, Next,End and Stop. This depends about were you are during the simulation or program execution.

• The Start command is used to start the program. The purpose is to change the control parameters.
  After selecting the Start command, the command changes into Cont.
• The Cont command is used to start the simulation.
  After selecting the Cont command is removed.
• The Next command is used to finish the simulation.
  The Display form shows the final result of the simulation. After selecting the Next command, the command changes into Start in order to start the next simulation.
• The End command is used to terminate the program
• The Stop command is used to stop the simulation

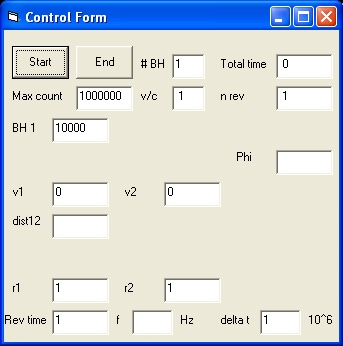Picture 1A

Picture 1A shows the control display in case of one BH and a lightray. The Control Form in case of 1 BH uses the following control paramaters: # BH , Max count , v/c , BH 1 , dist12 and freq The parameter # BH defines the number of Black Holes. #BH = 1 : One Black hole and a light ray. #BH = 2 : Two Black Holes. #BH = 3 : One binary Black Hole pair and a third smaller BH. In case of # BH = 1 the following control parameters are used: The parameter Max count defines the number of iterations in the first revolution. The parameter v/c defines the speed of the second object relative to the speed of light. The parameter BH 1 defines the mass of BH 1 in sun masses. The parameter dist12 defines the distance between object 1 and object 2. Because we study photons the distance is the radius of the circle. The parameter freq is the number of revolutions per second.

The Control Display also shows the following parameters:

• v1 this is the speed of the BH and is equal to zero.
• v2 this is the speed of the light ray.
• r1 the distance of the BH from the center of gravity. In this case = 0
• r2 the distance of the lightray from the center of gravity. In this case = dist12
• Rev time is Revolution time. In the case: 2 * pi * r / v with r = dist12 and v = v2.
• f = frequency. In this case f = 1/"Rev time"
• delta t is step size. In this case "Rev time"/"Max counter"

3.1 Operation - Control Form # BH = 1

In case # BH = 1 there are three ways to control the simulation.

1. Select BH 1 and v/c
   In that case the parameters dist12 and freq are calculated
   For Example:
   Select: "Start". Enter parameter # BH = 1. v/c = 1 . Select "Cont"

   Test	v/c	BH 1	dist12	f	total time
   1	1	10000	14766	3.23	.3095
   2	0.5	10000	59065	0.4	2.4758
   3	0.25	10000	236261	0.05	19.80
   4	1	200000	29532	1.61	.6189
   5	1	100	147.6	323.1	.003
   6	1	36+29	95.9	497.1	.002

   Select dist12 and BH 1
   In that case the parameters v/c and freq are calculated
   When the parameter v/c greater than one parameter v/c is set equal to 1 and the parameter BH 1 is also calculated.

   Test	dist12	BH 1	v/c	f	total time
   1	14766	10000	1	3.23	.3095
   2	20000	10000	.859	2.04	.4878
   3	50000	10000	.543	.51	1.9283
   4	10000	6772	1	4.77	.2095

   Select BH 1 and freq
   In that case the parameters v/c and dist12 are calculated
   When the parameter v/c greater than one parameter v/c is set equal to 1 and the parameter BH 1 is also calculated.

   Test	f	BH 1	v/c	dist12	total time
   1	3.23	10000	1	14766	.3095
   2	2	10000	.852	20331	.5
   3	1	10000	.852	32274	1
   4	5	6462	1	9542	.2

3.2 Operation - Control Form # BH = 2

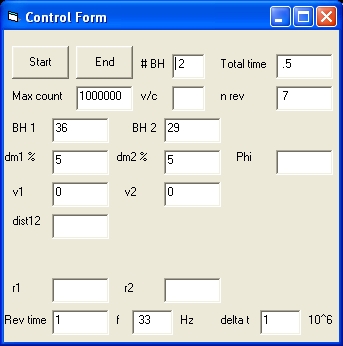
Picture 1B

Picture 1B shows the control display in case of two BH's The Control Form in case of 1 BH uses the following control parameters: # BH , Max count , v/c , BH 1 , BH 2 , dm1 % , dm2 % , dist12 and freq In case # BH = 2 there are three ways to control the simulation. Enter the parameters: BH 1 , BH 2 and v/c In that case the parameters: dist12 and freq are calculated. Enter the parameters: BH 1 , BH 2 and freq In that case the parameters: dist12 and v/c are calculated. Enter the parameters: BH 1 , BH 2 and dist12 In that case the parameters: v/c and freq are calculated.

3.3 Operation - Control Form # BH = 3

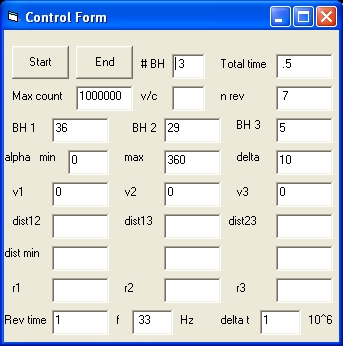Picture 1C

Picture 1C shows the control display in case of three BH's The Control Form in case of 1 BH uses the following control parameters: # BH , Max count , v/c , BH 1 , BH 2 , BH 3 , dist12 and freq alpha min, alpha max and delta In case # BH = 3 there are also three ways to control the simulation as explained above. The parameter alpha min defines the minimum angle of alpha. The standard value is 0. The parameter alpha max defines the maximum angle of alpha. The standard value is 360. The parameter delta defines the delta angle of alpha. The standard value is 10. when you use the standard values and you select "Start" the simulation will perform 36 simulations with the angles: 0,10,20 etc until 360 degrees. When alpha max = 0 you only will perform one simulation.

4. Display Form

The "Display Form" shows the result of the simulation.

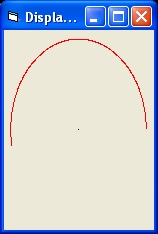
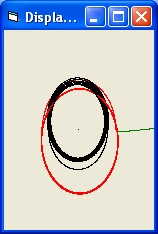
Picture 2A

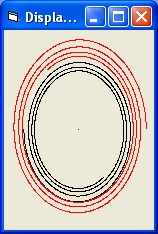
Picture 2B

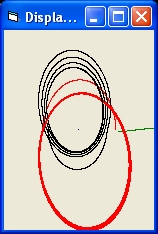
Picture 2C

Picture 2D

• Picture 2A shows the results of a simulation of 1 Black Hole and one light ray for one revolution.
  The initial display shows roughly the half of the first revolution.
  When the picture is selected you will observe the full revolution.
• Picture 2B shows the results of a simulation of 2 Black Holes for 7 revolutions.
  The largest BH (object 1) is in black. The smallest BH (object 2) is in red.
  The initial display shows roughly 3 revolutions.
  When the picture is selected you will observe the full 7 revolutions.
• Picture 2C shows the results of a simulation of 3 Black Holes for two angles:
  alpha = 0 and alpha = 180 degrees
  For the images of all angles between 0 and 360 degrees in increments of 10 degrees select Picture 2C. In this particular case mass of BH #3 = 5 solar masses

  Picture 2D shows the results of a simulation of 3 Black Holes for two angles:

  alpha = 0 and alpha = 180 degrees

  For the images of all angles between 0 and 360 degrees in increments of 10 degrees select Picture 2D. In this particular case mass of BH #3 = 10 solar masses

5. Program Evaluation with two Black Holes.

The purpose of these test is to observe the behaviour of 2 BH's
Test 1 is the galibration test

Test	BH 1	BH 2	dm1 %	dm2 %	v/c	n rev	dist12	nrev	freq	v1	v2
1	36	29	0	0	0.224	10	585.4	10	33	54095	67153
2	54.2	29	5	0	0.224	10	459.3	10	53.8	54095	100777
3	36	45	0	5	0.224	10	470.7	10	50.1	83978	67153
4	54.2	45	5	5	0.224	10	399.3	10	69.04	80383	97470
5	40	14.9	-2	-2	0.224	10	794.3	10	18.78	39915	49550

What the above table clearly indicate that when there is a positive influx of mass in a binary BH system the two will spiral together.
When there is a negative influx they will spiral apart.
This positive influx can be simulated by introducing a third large object.

5.1 Program evaluation with two Black Holes and a third large object.

BH1  36  BH2  29  BH3 5  nrev  10 alpha min  0  max  360  delta  10  v1  54157  v2  67229  v3  0 
 alpha   0 nBH 2 m1 40.9 m2 29.0 nrev 10 r1  238 r2  338 r3  382 d12 448 d13  93 d23 668 ttime 0.301 f 34.9
 alpha  10 nBH 2 m1 40.9 m2 29.0 nrev 10 r1  168 r2  239 r3  341 d12 371 d13 101 d23 648 ttime 0.241 f 44.5
 alpha  20 nBH 2 m1 40.9 m2 29.0 nrev 10 r1  128 r2  181 r3  321 d12 298 d13 110 d23 607 ttime 0.205 f 53.1
 alpha  30 nBH 2 m1 40.9 m2 29.0 nrev 10 r1  107 r2  151 r3  263 d12 255 d13 117 d23 555 ttime 0.188 f 58.5
 alpha  40 nBH 2 m1 40.9 m2 29.0 nrev 10 r1  100 r2  142 r3  196 d12 240 d13 121 d23 510 ttime 0.184 f 59.8
 alpha  50 nBH 2 m1 40.9 m2 29.0 nrev 10 r1  102 r2  145 r3  162 d12 246 d13 119 d23 484 ttime 0.191 f 57.0
 alpha  60 nBH 2 m1 40.9 m2 29.0 nrev 10 r1  113 r2  160 r3  141 d12 271 d13 113 d23 463 ttime 0.209 f 51.2
 alpha  70 nBH 2 m1 40.9 m2 29.0 nrev 10 r1  133 r2  188 r3  125 d12 308 d13 105 d23 438 ttime 0.243 f 42.8
 alpha  80 nBH 2 m1 40.9 m2 29.0 nrev 10 r1  179 r2  253 r3  192 d12 360 d13  94 d23 407 ttime 0.324 f 31.0
 alpha  90 nBH 2 m1 36.0 m2 33.9 nrev  1 r1  297 r2  314 r3  312 d12 518 d13  84 d23  57 ttime 0.500 f 32.5
 alpha 100 nBH 2 m1 36.0 m2 33.9 nrev  3 r1 1707 r2 1808 r3  278 d12 511 d13  89 d23  60 ttime 0.500 f  5.2
 alpha 110 nBH 2 m1 36.0 m2 33.9 nrev 10 r1  335 r2  355 r3  261 d12 500 d13 106 d23  70 ttime 0.487 f 20.0
 alpha 120 nBH 2 m1 36.0 m2 33.9 nrev  4 r1 2845 r2 3013 r3  605 d12 327 d13 127 d23  35 ttime 0.500 f 20.9
 alpha 130 nBH 2 m1 36.0 m2 33.9 nrev  4 r1  739 r2  784 r3  309 d12 452 d13  76 d23  57 ttime 0.500 f 12.1
 alpha 140 nBH 2 m1 40.9 m2 29.0 nrev 10 r1   51 r2   73 r3  344 d12 102 d13  98 d23  89 ttime 0.252 f 43.9
 alpha 150 nBH 2 m1 36.0 m2 33.9 nrev  2 r1 1736 r2 1838 r3  315 d12 529 d13 548 d23  60 ttime 0.500 f  4.9
 alpha 160 nBH 2 m1 36.0 m2 33.9 nrev  5 r1  820 r2  868 r3  378 d12 522 d13 607 d23  63 ttime 0.500 f 11.0
 alpha 170 nBH 2 m1 36.0 m2 33.9 nrev  9 r1  547 r2  580 r3  419 d12 496 d13 643 d23  68 ttime 0.500 f 19.5
 alpha 180 nBH 2 m1 36.0 m2 33.9 nrev 10 r1  294 r2  311 r3  452 d12 439 d13 654 d23  75 ttime 0.329 f 31.7
 alpha 190 nBH 2 m1 36.0 m2 33.9 nrev 10 r1  174 r2  184 r3  414 d12 328 d13 629 d23  86 ttime 0.231 f 46.7
 alpha 200 nBH 2 m1 36.0 m2 33.9 nrev 10 r1  110 r2  116 r3  297 d12 223 d13 557 d23 101 ttime 0.181 f 61.6
 alpha 210 nBH 2 m1 40.9 m2 29.0 nrev 10 r1   46 r2   65 r3  373 d12 104 d13 102 d23 127 ttime 0.225 f 48.6
 alpha 220 nBH 2 m1 40.9 m2 29.0 nrev 10 r1  154 r2  219 r3  489 d12 322 d13  80 d23 152 ttime 0.481 f 20.3
 alpha 230 nBH 2 m1 40.9 m2 29.0 nrev  3 r1 1330 r2 1881 r3  412 d12 444 d13  70 d23 169 ttime 0.500 f  5.6
 alpha 240 nBH 2 m1 40.9 m2 29.0 nrev  2 r1  496 r2  703 r3  350 d12 454 d13  70 d23 181 ttime 0.500 f  4.0
 alpha 250 nBH 2 m1 40.9 m2 29.0 nrev  4 r1  358 r2  505 r3  292 d12 459 d13  72 d23 191 ttime 0.500 f  6.5
 alpha 260 nBH 2 m1 40.9 m2 29.0 nrev  6 r1  324 r2  459 r3  228 d12 459 d13  78 d23 205 ttime 0.500 f 12.7
 alpha 270 nBH 3 m1 36.0 m2 29.0 nrev 10 r1  305 r2  379 r3 7103 d12 239 d13 117 d23 232 ttime 0.229 f 44.7
 alpha 280 nBH 2 m1 40.9 m2 29.0 nrev  7 r1  888 r2 1255 r3  289 d12 317 d13  74 d23 275 ttime 0.500 f  9.1
 alpha 290 nBH 2 m1 39.2 m2 29.0 nrev 10 r1  291 r2  394 r3  238 d12 180 d13 113 d23 336 ttime 0.251 f 52.4
 alpha 300 nBH 2 m1 39.0 m2 29.0 nrev 10 r1  164 r2  221 r3  263 d12 147 d13 110 d23 292 ttime 0.255 f 49.5
 alpha 310 nBH 2 m1 36.0 m2 33.9 nrev 10 r1  119 r2  126 r3  399 d12 128 d13  83 d23  76 ttime 0.286 f 34.8
 alpha 320 nBH 2 m1 40.9 m2 29.0 nrev  6 r1  571 r2  807 r3  294 d12 531 d13  78 d23 545 ttime 0.500 f 12.1
 alpha 330 nBH 2 m1 40.9 m2 29.0 nrev  7 r1  390 r2  552 r3  288 d12 531 d13  79 d23 599 ttime 0.500 f 15.1
 alpha 340 nBH 2 m1 40.9 m2 29.0 nrev  9 r1  396 r2  560 r3  375 d12 517 d13  82 d23 639 ttime 0.500 f 19.3
 alpha 350 nBH 2 m1 40.9 m2 29.0 nrev 10 r1  335 r2  474 r3  397 d12 493 d13  86 d23 664 ttime 0.394 f 26.0
 alpha 360 nBH 2 m1 40.9 m2 29.0 nrev 10 r1  234 r2  333 r3  399 d12 448 d13  93 d23 668 ttime 0.301 f 34.9

• The parameter d12 shows the nearest distance between object 1 and 2.
  The closest distance are simulated with alpha = 140 and alpha= 210.
• The parameter f shows the frequency between object 1 and object 2.
  The higest frequency are simulated with alpha = 40 and alpha= 290.

The following table shows the results for mass of BH #3 = 10 solar masses.

BH1  36  BH2  29  BH3 10  nrev  10 alpha min  0  max  360  delta  10  v1  54157  v2  67229  v3  0 
 alpha   0 nBH 2 m1 45.9 m2 29.0 nrev 10 r1   245 r2   390 r3  395 d12 372 d13  84 d23 655 ttime 0.406 f 26.2
 alpha  10 nBH 2 m1 45.9 m2 29.0 nrev 10 r1   125 r2   201 r3  326 d12 261 d13  91 d23 647 ttime 0.232 f 48.9
 alpha  20 nBH 2 m1 45.9 m2 29.0 nrev 10 r1    74 r2   120 r3  299 d12 163 d13  99 d23 618 ttime 0.169 f 70.5
 alpha  30 nBH 2 m1 44.6 m2 29.0 nrev 10 r1    48 r2    76 r3  312 d12 109 d13 105 d23 579 ttime 0.145 f 81.6
 alpha  40 nBH 2 m1 44.1 m2 29.0 nrev 10 r1    50 r2    77 r3  221 d12  86 d13 107 d23 543 ttime 0.139 f 84.6 
 alpha  50 nBH 2 m1 44.7 m2 29.0 nrev 10 r1    45 r2    71 r3  188 d12  85 d13 105 d23 521 ttime 0.147 f 78.8
 alpha  60 nBH 2 m1 36.0 m2 38.9 nrev  1 r1 33238 r2 30682 r3  410 d12 460 d13  95 d23  49 ttime 0.500 f 35.8
 alpha  70 nBH 2 m1 36.0 m2 38.9 nrev  1 r1 30746 r2 28382 r3  382 d12 472 d13  93 d23  51 ttime 0.500 f 34.9
 alpha  80 nBH 2 m1 36.0 m2 38.9 nrev  1 r1 28772 r2 26560 r3  351 d12 480 d13  87 d23  52 ttime 0.500 f 33.8
 alpha  90 nBH 2 m1 36.0 m2 38.9 nrev  1 r1 27311 r2 25210 r3  327 d12 480 d13  80 d23  53 ttime 0.500 f 32.4
 alpha 100 nBH 2 m1 36.0 m2 38.9 nrev  1 r1 25123 r2 23192 r3  303 d12 474 d13  74 d23  55 ttime 0.500 f 31.2
 alpha 110 nBH 2 m1 36.0 m2 38.9 nrev  1 r1 18274 r2 16870 r3  272 d12 460 d13  72 d23  58 ttime 0.500 f 32.0
 alpha 120 nBH 3 m1 36.0 m2 29.0 nrev 10 r1   136 r2   169 r311725 d12  97 d13  81 d23  87 ttime 0.154 f 71.6
 alpha 130 nBH 2 m1 36.0 m2 38.9 nrev  3 r1   980 r2   906 r3  121 d12 140 d13 112 d23  74 ttime 0.500 f  4.4
 alpha 140 nBH 2 m1 44.5 m2 29.0 nrev 10 r1   281 r2   433 r3  170 d12 242 d13 105 d23 137 ttime 0.392 f 45.6
 alpha 150 nBH 1 m1 37.5 m2 29.0 nrev  1 r1    19 r2    28 r3  282 d12  48 d13  89 d23  62 ttime 0.048 f 44.8
 alpha 160 nBH 2 m1 36.0 m2 38.9 nrev  0 r1 23161 r2 21379 r3  358 d12 552 d13 563 d23  56 ttime 0.500 f 32.9
 alpha 170 nBH 2 m1 36.0 m2 38.9 nrev  0 r1 10439 r2  9636 r3  395 d12 552 d13 617 d23  60 ttime 0.500 f 32.9
 alpha 180 nBH 2 m1 36.0 m2 38.9 nrev  7 r1   785 r2   725 r3  440 d12 371 d13 642 d23  67 ttime 0.500 f 15.6
 alpha 190 nBH 2 m1 36.0 m2 38.9 nrev 10 r1   131 r2   121 r3  437 d12 218 d13 632 d23  76 ttime 0.236 f 48.1
 alpha 200 nBH 2 m1 36.0 m2 37.5 nrev 10 r1    47 r2    44 r3  353 d12  85 d13 580 d23  87 ttime 0.144 f 82.5
 alpha 200 nBH 2 m1 36.0 m2 38.9 nrev 15 r1    53 r2    47 r3  342 d12  82 d13 581 d23  87 ttime 0.203 f 86.2
 alpha 210 nBH 1 m1 45.9 m2 29.0 nrev  1 r1    33 r2    53 r3  555 d12  86 d13  74 d23 112 ttime 0.210 f 45.3
 alpha 220 nBH 2 m1 45.9 m2 29.0 nrev  1 r1 18056 r2 28639 r3  492 d12 311 d13  64 d23 137 ttime 0.500 f 43.5
 alpha 230 nBH 2 m1 45.9 m2 29.0 nrev  1 r1 22159 r2 35149 r3  457 d12 339 d13  62 d23 155 ttime 0.500 f 41.7
 alpha 240 nBH 2 m1 45.9 m2 29.0 nrev  1 r1 20910 r2 33165 r3  362 d12 360 d13  63 d23 166 ttime 0.500 f 39.8
 alpha 250 nBH 2 m1 45.9 m2 29.0 nrev  1 r1 16756 r2 26579 r3  298 d12 373 d13  67 d23 171 ttime 0.500 f 38.5
 alpha 260 nBH 2 m1 45.9 m2 29.0 nrev  1 r1  5745 r2  9113 r3  246 d12 381 d13  74 d23 174 ttime 0.500 f 37.7
 alpha 270 nBH 3 m1 36.0 m2 29.0 nrev 10 r1   326 r2   404 r3 3906 d12 102 d13 104 d23 177 ttime 0.193 f 54.4
 alpha 280 nBH 2 m1 36.0 m2 33.8 nrev 10 r1   345 r2   367 r3  246 d12 122 d13 152 d23  77 ttime 0.221 f 42.3
 alpha 290 nBH 2 m1 36.0 m2 37.7 nrev 10 r1   317 r2   302 r3  200 d12 118 d13 237 d23 103 ttime 0.201 f 63.8
 alpha 300 nBH 2 m1 45.9 m2 29.0 nrev  2 r1 17950 r2 28470 r3  308 d12 361 d13  66 d23 236 ttime 0.500 f 14.8
 alpha 310 nBH 2 m1 44.6 m2 29.0 nrev 10 r1   122 r2   190 r3  320 d12 262 d13  98 d23 227 ttime 0.220 f 63.6
 alpha 320 nBH 2 m1 36.0 m2 36.6 nrev 10 r1   249 r2   244 r3  125 d12 154 d13  73 d23  74 ttime 0.171 f 77.8
 alpha 330 nBH 2 m1 45.9 m2 29.0 nrev  0 r1 11461 r2 18179 r3  308 d12 555 d13  72 d23 544 ttime 0.500 f 32.9
 alpha 340 nBH 2 m1 45.9 m2 29.0 nrev  0 r1  5001 r2  7934 r3  313 d12 553 d13  74 d23 601 ttime 0.500 f 32.9
 alpha 350 nBH 2 m1 45.9 m2 29.0 nrev  4 r1   832 r2  1320 r3  377 d12 441 d13  78 d23 639 ttime 0.500 f  9.2
 alpha 360 nBH 2 m1 45.9 m2 29.0 nrev 10 r1   245 r2   390 r3  390 d12 372 d13  84 d23 655 ttime 0.406 f 26.2

• The parameter r1 and r2 show the final distance of the objects #1 and #2.
  In 10 cases the distance is roughly 5000 or more, which implies that as a result of the merging of object #3 with either object #1 or object #2, both are ejected.
  This is the case with alpha: 60,70,80,90,100,110,160,170,220,230,240,250,260,300, 330 and 340.
• The shortest distance between object #1 and #2 d12 is at alpha 150 = 48.
• The higest frequence is at alpha 40 = 84.6

6 Simulation of BH merger

Picture 3

Picture 3 shows a simulation of a BH merger of 2 BH's and a third object of 12 solar masses Object 3 first merges with BH #1. This is the largest BH. After this the object evaporates. The merging start when the third object reaches a speed above the speed of light. This is the largest BH and then two BH's spiral together. When Picture 3 is selected you will see the Control form at the end of the simulation. It is the smallest BH #2 that will reach the final speed of 300000 km/sec. That means the smallest BH in a sense that collides with the largest BH. What you can also see from the Control Form that the rotation frequency of the two BH's, which started at 33 HZ at the end was 88 HZ. In order to perform the simulation the following parameters are selected: # BH = 3, BH 1 = 36, BH 2 = 29, BH 3 = 12. n rev = 0. Total time = 0.5 sec alpha min = 40 or 50 alpha max = 0 and f = 33 Hz

7. VB2019 Simulation of Binary Black Hole system, circulated by a third star

Picture 4a Test 5 and Test 7

Picture 4b Test 10 and Test 9

The Pictures 4A and 4B shows a simulation of a binary system of 2 BH's of 20 solar masses each, and a third small star, which circulates around both these BH's. The distance of the small star in each frame is different The simulation is performed under four different situations or tests. Pictures 4A shows the tests 5 and 7. Pictures 4B shows the tests 9 and 10. In Test 5 the third star has the largest radius. In Test 10 the third star has the smallest radius. The Radius of Test 7 and Test 9 is in between Test 5 and Test 10. As mentioned, Test 5 the third star has the largest radius. The center of the picture shows the 2 black holes circulating around each other. This is a stable configuration. The picture also shows a third object in green. This object cycles in a circle around the 2 objects. In Test 5 the radius is large and the third object moves in a stable configuration around the center of gravity of the two Black holes. In Test 7 the radius is smaller as in Test 5 and the third object moves in a stable configuration around the center of gravity of the two Black holes. To observe Test 7 select Pictures 4A In Test 9 the radius is smaller as in Test 7 large and the third object moves in a stable configuration around the center of gravity of the two Black holes. To observe Test 9 select Pictures 4B In Test 10 the radius is smallest and the third object moves in an unstable manner around the center of gravity of the two Black holes. When the radius is slightly smaller as in Test 10 the third object will be ejected from the binary system.

• In order to explain the situation it is first important to study a simpler situation. That is the situation when you combine the 2 BH's of 20 solar masses each, in one with 40 solar masses and a second star the same as before. That star will be attracted by the BH and when it has the right force perpendicular to this force in the direction of movement it will also cycle in a 'straight' circle around the BH in the centre. In this case that the gravitational field of one black hole is static.
  
• Compared with the gravitational field of two black holes, circulating around each other, the field is dynamic. The result is that movement of the third object also follows a circle, but that circle is an approximation and posseses a wobble. In reality you can speak of a superposition of two wobbles:
  • The first wobble is caused because the third star moves around the two black holes. This wobble has a low frequency.
  • The second wobble is caused because the two blackholes move around each other. This wobble has a higher frequency.
    The second wobble is the best indication that the gravitational field propagates in space as gravitational waves.

Picture 5a Test 5 and 7 Picture 5b Test 10 and 9

The Pictures 5A and 5B shows a simulation of a binary system of 2 BH's of 20 solar masses each, and a third small star. The emphasis is on the radius of the third object, the object that revolves around the 2 BH's. Figure 5A shows the Tests 5 and 7. These have the largest radia. They can be called stable. Figure 5B shows the Tests 10 and 9. These have the smallest radia. They can be called unstable. Test 5 shows the configuration that distance between the third object and the center center of gravity is the largest. The display shows two revolutions of the third object. The shape shows two slow wobbles and for the rest the shabe is 'flat'. The behavior is stable. Test 7 shows the configuration that distance between the third object and the center center of gravity is smaller than Test 5. The display shows three revolutions of the third object. The shape shows the same slow wobbles caused the the third object revolving are the two BH's, but also the faster wobbles caused by the two BH's. The behavior is stable. Test 9 shows the configuration that distance between the third object and the center center of gravity is smaller as in Test 7. The display shows three revolutions of the third object. The shape shows the same slow wobbles caused the the third object revolving are the two BH's, but also the faster wobbles caused by the two BH's. The behavior is stable. Test 10 shows the configuration that distance between the third object and the center center of gravity is smaller as in Test 7. The display shows three revolutions of the third object. The shape shows the same slow wobbles caused the the third object revolving are the two BH's, but also the faster wobbles caused by the two BH's. The behavior is stable.

Picture 5a Test 5 and 7

Picture 5b Test 10 and 9

• The parameter r3 shows the radius of the third object.
  The average value in Test 5 = 820, in Test 7 = 630, in Test 9 = 560 and in Test 10 = 500 and decreasing.
• The parameters v3min and v3max show the minimum and maximum speed of the third values.
  The value of v3max in Test 5 = 83400, in Test 7 = 98200, in Test 9 = 11500 and in Test 10 = 12700 and increasing.
• The parameter nrev3 shows the number of revolutions of the third object. In test 5, 7, 9 and 10 the values are 2, 2, 3 and 4
• The parameter mul34 defines the radius r3/r1 or r3/r2

Reflection 1 - Overall evaluation of this simulation

The behaviour of the BH's or objects in the simulation is partly controlled by the speed of light. Physical considerations limitate that no object can move with a speed higher than the speed of light. That means, if an object reaches the speed of light, it will physical desintegrate. The most probably candidate for this behaviour is the third object. The simulation of the process involved can also be done at lower speeds. This means there is a chance that the whole process of desintegration does not happen
More important is that the explanation of the behaviour lies in fact that objects influence each other or more accurate that they attract each other that means we can explain the behaviour by introducing forces, including the merging of objects. Forces are used to explain more physical processes i.e. electromagnetic, weak and strong force. This explanation has nothing to do with light (photons) nor with the behaviour of physical clocks. You can ask your self the question why is that.

A different explanation for the behaviour is to introduce concepts like: the curvature of space and time or the curvature of spacetime. But that requires a clear definition of each, which does not exist. The problem is that the concept of curvature only makes sense in relation to the physical shape of objects. For example: A statue shows curvature. This allows us to consider that the shape of the earth is not exactly round but is curved. The importance is limited.
When you observe images of gravitational waves around two blackholes. The shape are spirals which start at the present positions of the two BH's and move outwards. It is interesting to realize the positions of the waves further away, represent the state of the BH's in the past. See also below.
Normally only one lightray is shown to indicate that its path is not straight but bended. In reality this picture is extremely more complex because at each instant from all directions (and distances) around the two BH's, light is approaching, merging and disappearing in all directions.

A different problem are the concepts the present, universal time and clock time related to the evolution of the Universe.
At any moment in time the whole universe is in a certain state. This moment we can call the present . What is also important that at any moment the state of the universe is changing, specific the positions of all what we call matter, at all levels of detail. The origin of these changes is caused by all the objects, which influence each other.
We humans can the define the past and future, and a time line. The time line shows the universal time. This line starts some where in the past, is now at a position we call the present and continues in the future. The importance of this time line is, that all events happening at the same position are happening simultaneous.

It is important that all what each human observer sees at present, does not reflect what is happening at present in the universe. The simple reason is that all what we see at present has happened in the past. This is, because it takes time for the light signals, which are created at events in the past, reach our eyes.
It may seem strange, but IMO the concept clock time, which shows number on a mechanical device we call clock, has nothing to do with the evolution of any process in the universe except with the behaviour of the mechanical device it self. That

Reflection 2 - Gravitational waves - three questions

1. The first question, behind the simulation of the two BH's, around which a third objects circulates, is supposed two answer two questions:
   • Are the two BH's together emitting gravitational waves and:
   • Is the simulation a demonstration that this is actual the case
   IMO this depends very much about the definition of what is a gravitational wave. IMO what the two BH's do is they produce a varying gravitational field around each BH which radiates in space which each a BH in its center. The circulating object is a demonstration of of this varying gravitational field.
2. The second question is: emit the stars which circulate around the BH in the center of the solar system also emit gravitational waves, in a similar manner as the 2 BH's part of question 1? For more detail about this simulation select this link: VB2019 Sagittarius A* simulation In this simulation it is the fast oscillating star S62 which introduces the wobbles in the slow oscillating star S1.
   This can be compared with the fast oscillations of the two BH's which introducing the wobbles in the slow oscillating third star.
   
3. A similar situation exist when influence of the fast oscillations of the planet Mercury are compared with the slow oscillations and the movement of the Earth. These wobbles show the same behaviour compared with the third object, studied previous.
   In reality the influence of the Earth on the planet Mercury is much stronger, but that is not the issue.

Reflection 3 - Does the concept: "Gravitational waves" makes sense ?

My understanding is that all material objects are surrounded by a gravitational field. This field defines the strength of the force of attraction of an object with mass m, enforced on an object of mass 1. This field is not something that physical exists, but that is not the issue. This field is the stronger, the closer the distance between the two objects is. Both objects attract each other.
In the litterature the most common discussed situation are two binary stars (with each the same mass m). General speaking these systems are considered stable. Sometimes this is not the case. In these cases the two stars are different and the result is a constant flow of matter from one star two the other star, which causes one slowly to disappear.

However with BH's the situation is considered different. The general opinion is that a configuration of 2 BH's is unstable because they emit gravitational waves, as a result the 2 BH's loose energy and mass, which causes them to merge. This merging is detected par example by Ligo.
However I doubt this theory. In my opinion when in some way the 2 BH's are unstable, always a third star is involved. That is the situation described in 6 Simulation of BH merger

Feedback

Back to my home page: Contents of This Document